투포인터 알고리즘
리스트나 배열에 순차적으로 접근해야 할 때, 두 개의 점의 위치를 기록하면서 처리하는 알고리즘
1. 원리
1. 시작점과 끝점이 첫번째 원소의 인덱스를 가르키도록 한다.
2. 목표값 보다 시작점 인덱스부터 끝점의 인덱스까지의 결과값이 작으면 끝점(end)를 1 증가시킨다.
3. 목표값 보다 시작점 인덱스부터 끝점의 인덱스까지의 결과값이 크거나 같으면 시작점(start)를 1 증가시킨다.
4. 모든 경우를 확인할 때가지 2~3번 과정을 반복한다.
2. 예제
예제를 통해 알아보자.
투포인터 알고리즘의 대표적인 문제인 특정한 합을 가지는 부분 연속 수열 찾기로 알아보자.
아래와 같은 수열이 있다.

여기서 연속되는 수의 합이 5 일때의 개수를 구해보자.
투포인터 알고리즘을 사용하면 다음과 같은 로직을 따른다.
1. 시작점과 끝점이 첫번째 원소의 인덱스(0)를 가리키도록 한다.
2. 현재 부분 합이 5와 같다면 카운트한다.
3. 현재 부분 합이 5보다 작다면 끝점(end)를 1 증가시킨다.
4. 현재 부분 합이 5보다 크거나 같다면 start를 1 증가시킨다.
5. 모든 경우를 확인할 때까지 2~4번 과정을 반복한다.
그림으로 설명하면 이해가 더 빠를것이다.
[step1] 시작점과 끝점이 첫번째 원소의 인덱스를 가리키도록 함

- 현재의 부분 합: 1
- 부분 합이 5가 아니므로 카운트는 0
[step2] 부분 합이 5보다 작으므로 끝점(e)를 1 증가시킴.

- 현재 부분 합: 3
- 부분 합이 5보다 작으므로 카운트는 0
[step3] 부분 합이 5보다 작으므로 끝점(e)를 1 증가시킴.

- 현재 부분 합: 6
- 부분 합 > 6 이므로 카운트는 0
[step4] 부분 합(6) > 5 이기에 시작점(s)를 1 증가시킴. (이때 중요한 점이, 부분 합에서 시작점을 증가시키기 전 인덱스에 해당하는 값을 빼줘야한다!)

- 부분 합: 5
- 부분합 = 5 이므로 카운트는 1
[step5] 부분 합(5) = 5 이기에 시작점을 1 증가시킴. (마찬가지로 부분 합에서 2를 빼줘야한다.)

- 부분 합: 3
- 부분 합 < 5이므로 카운트는 그대로 1
[step6] 부분 합(3) < 5 이기에 끝점을 1 증가시킴.
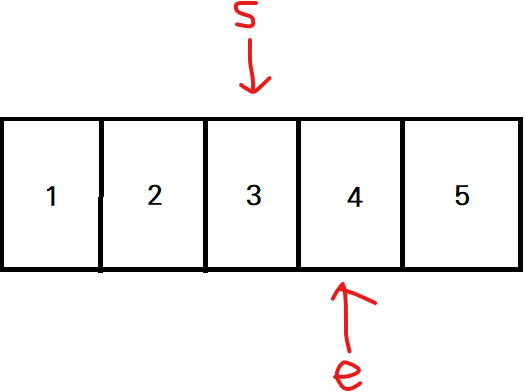
- 부분 합: 7
- 부분 합 > 5 이므로 카운트는 그대로 1
[step7] 부분 합(7) > 5 이기에 시작점을 1 증가시키고, 부분 합에서 3을빼줌.
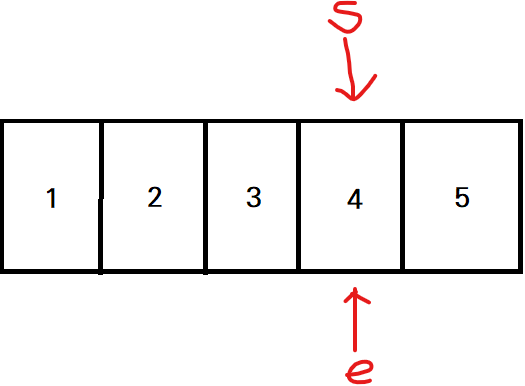
- 부분 합: 4
- 부분 합 < 5 이므로 카운트는 그대로 1
[step8] 부분 합(4) < 5 이기에 끝점을 1 증가시킨다.
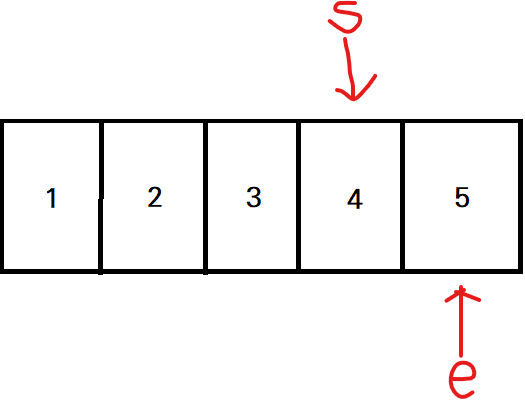
- 부분 합: 9
- 부분 합 > 5 이므로 카운트는 그대로 1
[step9] 부분 합(9) > 5 이기에 시작점을 1 증가시키고, 부분 합에서 4를 뺴줌
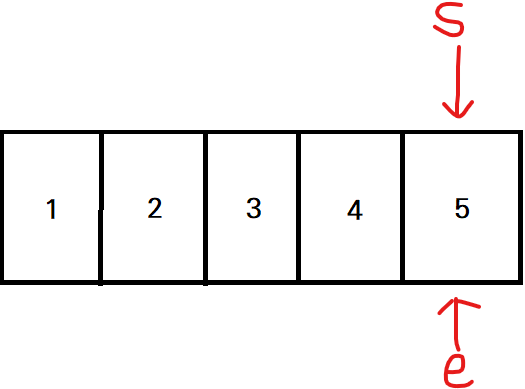
- 부분 합: 5
- 부분 합 = 5 이므로 카운트 +1 (총: 2)
[end] 시작점과(s) 끝점(e)이 마지막 인덱스에 도달했기 때문에 탐색을 종료한다.
3. 코드
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
int N = 5;
int M = 5;
int[] numbers = {1,2,3,4,5};
int sum = 0;
int count = 0;
int end = 0;
for(int start = 0; start < N; start++) {
// 부분합이 M보다 작을 때 end 1 증가
while(sum < M && end < N) {
sum += numbers[end];
end++;
}
// 부분합이 M일땐 count 1 증가
if(sum == M) count++;
// while 반복문이 모두 끝나고 부분합이 M보다 클 때
sum -= numbers[start];
}
System.out.println(count);
}
}import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
int N = 5;
int M = 5;
int[] numbers = {1,2,3,4,5};
int count = 0;
int start = 0;
int end = 0;
int sum = 0;
while (end < N) {
sum += numbers[end];
end++;
while (sum >= M) {
if(sum == M) count++;
sum -= numbers[start];
start++;
}
}
System.out.println(count);
}
}4. 예시문제 추천(백준)
https://www.acmicpc.net/problem/2003
2003번: 수들의 합 2
첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.
www.acmicpc.net
 Reference
Reference'Algorithm > KBro Study' 카테고리의 다른 글
| [알고리즘] LCS(최장 공통 부분 수열) & LIS(가장 긴 증가하는 부분 수열) (0) | 2023.03.27 |
|---|---|
| [알고리즘] Dynamic Programming(동적 계획법) (0) | 2023.03.17 |
| [알고리즘] 벨만포드 알고리즘 (Bellman-Ford) (0) | 2023.03.02 |
| [알고리즘] 그리디 - 최소 스패닝 트리(Minimum Spanning Tree) (0) | 2023.02.19 |
| [자료구조] 그래프(Graph) + 구현하기(Java의 인접행렬과 인접리스트) (0) | 2023.01.17 |