그리디(Greedy) 알고리즘
들어가기에 앞서, 그리디 알고리즘에 대해 간략히 알아보자.
그리디(탐욕) 알고리즘 이란?
=> 매 선택에서 지금 이 순간 당장 최적인 답을 선택하여 적합한 결과를 도출하는 알고리즘이다. = 탐욕 알고리즘
빠르지만, 항상 최적인 답이라는 보장은 없다.
Union-Find 알고리즘
Disjoint-set(서로소 집합)을 표현하기 위해 사용하는 알고리즘
ex) {1,2} {3,4} → 서로소, {1,2} {2,3} → 서로소 아님
(1). Union
2개 원소로 이루어진 집합을 하나의 집합으로 합치기
ex) {1} + {2} → {1,2}
(2). Find
특정 원소가 속한 집합이 뭔지 알려주는 연산
ex) Find({ {1,2,3}, {4,5}, {10} }, 2) → {1,2,3}
동작 과정
- union 연산: 서로 연결된 두 노드 A, B에 대하여(2) A'를 B'의 부모 노드로 설정 (A' < B')
- (1) A의 루트 노드 A'과 B의 루트 노드 B'를 찾기(find)
- 모든 union 연산을 처리할 때까지 1 반복
ex) {1,2,3,4,5,6}의 집합과 4개의 union연산 union 1,4 union 2,3 union 1,2 union 5,6이 주어졌을 때, Union-Find 알고리즘의 결과를 그래프로 나타내면 다음과 같다.

자세한 동작 과정은 아래 표와 같다.
1. 초기화

2. union 1,4

3. union 2,3

4. union 1,2

5. union 5,6

이를 python 코드로 직접 구현하면 아래와 같다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
return find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
p_a = find_parent(parent, a)
p_b = find_parent(parent, b)
if a < b:
parent[p_b] = p_a
else:
parent[p_a] = p_b
class a{
static int[] parent;
public static int find(int n){
if(n == parent[n]) return n;
return parent[n] = find(parent[n]);
}
public static void union(int a, int b){
int pA = find(a);
int pB = find(b);
if(pA != pB){
parent[b] = parent[a];
}
}
public static void main(String[] args){
int n = 6;
parent = new int[n+1];
for(int i=1; i<=n; i++){
parent[i] = i;
}
union(1,4);
union(2,3);
union(1,2);
union(5,6);
union(4,1);
int mumo = find(3); // 1
}
}
이후 kruskal MST에서 두 노드를 연결할 때, 사이클이 생기는지 확인하기 위해 이 알고리즘을 사용한다.
Mimimum Spanning Tree(최소 신장 트리)
Spanning Tree: 그래프 내의 모든 정점을 포함하는 트리
MST: Spanning Tree중에서 사용된 간선들의 가중치 합이 최소인 트리
(1) MST의 특징
- 간선의 가중치의 합이 최소여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
- 사이클이 포함되어서는 안된다.
(2) 사용 사례
통신망, 도로망, 유통망에서 길이, 구축 비용, 전송 시간 등을 최소로 구축하려는 경우에 사용한다.
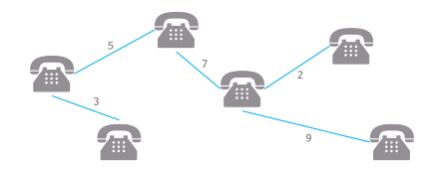
최소 스패닝 트리(최소 신장 트리)는 신장 트리에서 가중치의 합이 최소인 것을 말한다.
여기서 신장 트리란, n 개의 정점으로 이루어진 무방향 그래프 G 에서 n 개의 모든 정점과 n-1개의 간선으로 만들어진 트리를 말한다.(최소의 간선으로 모든 정점을 연결한 그래프)


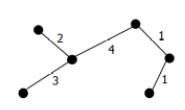
주어진 가중치 그래프에서 사이클 없이 모든 점을 연결시키면 신장 트리가 되는데, 이러한 종류의 트리들 중 가중치의 합이 최소는 아니다.
최소 신장 트리를 찾는 대표적인 그리디 알고리즘은 아래와 같다.
- 크루스칼 알고리즘(Kruskal's Algorithm)
- 프림 알고리즘(Prim's Algorithm)
MST 구현
1. Kruskal MST
greedy method를 이용하여 가중치를 간선에 할당한 그래프의 모든 정점을 최소 비용으로
연결하여 최적의 답을 찾는 방법
특징
- 시간복잡도 : O(ElogE) => E는 입력 그래프에 있는 간선의 수
- 간선이 적은 경우에 적합
과정
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
- 사이클을 형성하는 간선을 제외한다. (Union-Find 알고리즘으로 확인)
3. 해당 간선을 현재의 MST의 집합에 추가한다
이를 그래프 예제로 나타내면 다음과 같다.

(백준 1197) Kruskal MST로 구현한 python코드는 다음과 같다.
문제(BOJ 1197)
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.

코드
def find_parent(parent,x):
if parent[x] != x:
parent[x] = find_parent(parent,parent[x])
return parent[x]
def union_parent(parent,a,b):
a = find_parent(parent,a)
b = find_parent(parent,b)
if a < b:
parent[b] = a
else:
parent[a] = b
#------ 사이클 판별을 위한 Union-Find 알고리즘 ------#
answer = 0
v,e = map(int,stdin.readline().split())
graph = []
parent = {node:node for node in range(1,v+1)}
for _ in range(e):
a,b,c = map(int,stdin.readline().split())
graph.append((a,b,c))
# 1.간선들을 오름차순으로 정렬
graph = sorted(graph,key=lambda x:x[2])
for s,e,w in graph:
# 2.사이클 형성이 안 되는 간선 선택
if find_parent(parent,s) == find_parent(parent,e):
continue
# 3. 해당 간선을 현재 집합에 추가
union_parent(parent,s,e)
answer += w
print(answer)2. Prim 알고리즘
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법
특징
- 시간복잡도 : Min-Heap: O(ElogE) / 최악: O(n^2)
- 간선이 많은 경우에 적합
과정
- 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
- 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
3. 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다. (N == 정점의 갯수)
이를 그래프 예제로 나타내면 다음과 같다.

(백준 1922) Prim MST로 구현한 python코드는 다음과 같다.
문제(BOJ 1922)
도현이는 컴퓨터와 컴퓨터를 모두 연결하는 네트워크를 구축하려 한다. 하지만 아쉽게도 허브가 있지 않아 컴퓨터와 컴퓨터를 직접 연결하여야 한다. 그런데 모두가 자료를 공유하기 위해서는 모든 컴퓨터가 연결이 되어 있어야 한다. (a와 b가 연결이 되어 있다는 말은 a에서 b로의 경로가 존재한다는 것을 의미한다. a에서 b를 연결하는 선이 있고, b와 c를 연결하는 선이 있으면 a와 c는 연결이 되어 있다.)
그런데 이왕이면 컴퓨터를 연결하는 비용을 최소로 하여야 컴퓨터를 연결하는 비용 외에 다른 곳에 돈을 더 쓸 수 있을 것이다. 이제 각 컴퓨터를 연결하는데 필요한 비용이 주어졌을 때 모든 컴퓨터를 연결하는데 필요한 최소비용을 출력하라. 모든 컴퓨터를 연결할 수 없는 경우는 없다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.

코드
from sys import stdin
import heapq as hq
n = int(stdin.readline())
m = int(stdin.readline())
answer = 0
q = []
visit = {node:0 for node in range(1,n+1)}
graph = {node:{} for node in range(1,n+1)}
count = 0
for _ in range(m):
a,b,c = map(int, stdin.readline().split())
graph[a][b] = graph[b][a] = c
hq.heappush(q,(0,1)) #시작 노드
while count <= n-1:
value,node = hq.heappop(q)
if visit[node] == 1:
continue
count += 1
answer += value
visit[node] = 1
for adj_node,adj_value in graph[node].items():
hq.heappush(q,(adj_value,adj_node))
print(answer)
📗참고사이트
'Algorithm > KBro Study' 카테고리의 다른 글
| [알고리즘] Dynamic Programming(동적 계획법) (0) | 2023.03.17 |
|---|---|
| [알고리즘] 벨만포드 알고리즘 (Bellman-Ford) (0) | 2023.03.02 |
| [자료구조] 그래프(Graph) + 구현하기(Java의 인접행렬과 인접리스트) (0) | 2023.01.17 |
| [알고리즘] Brute Force(브루트 포스) (0) | 2023.01.08 |
| [자료구조] B-tree, B+tree 이론 정리 (0) | 2022.12.28 |
![[알고리즘] 그리디 - 최소 스패닝 트리(Minimum Spanning Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdC3jBB%2FbtrZNvmhKHt%2F84qKPqosuAjf0EGSlkI3t1%2Fimg.png)